Research
Non-perturbative Cavity Quantum Electrodynamics
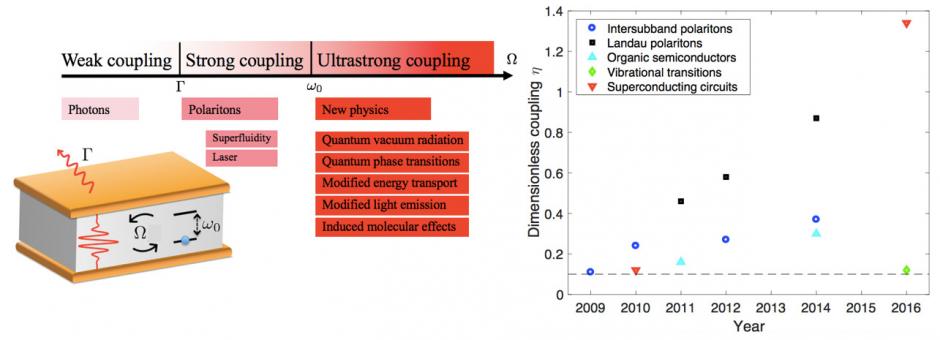
Left: scheme of a cavity quantum electrodynamics setup and of its different regimes. When the light-matter coupling Ω becomes larger than the losses Γ, the system is said to be in the strong coupling regime, which becomes ultrastrong when Ω becomes comparable to the bare frequency ω0. Right: some values from milestone observations of record values of the dimensionless coupling η=Ω/ω0 are shown for different CQED systems, since the first observation in 2009. The dashed line marks the value η=0.1, often used as conventional threshold of the ultrastrong coupling.
Cavity quantum electrodynamics investigates the interaction of matter with single photons ensnared in a cavity. In the first pioneering experiments which won S. Haroche and D. Wineland a Nobel prize, the role of matter was played by single atoms or ions. Solid-state implementations soon followed and cavity quantum electrodynamics experiments are now routinely performed on many platforms, ranging from microcavity embedded quantum wells, to magnons, to superconducting circuits. In these implementations, thanks to the phenomenon of superradiance [1], the large dipole density achievable in solid-state systems allowed the strength of the coupling between light and matter to be dramatically increased.
The coupling between light and matter is usually weak enough to be intuitively described in terms of the emission and absorption of photons, while the matter system jumps between two of its quantised eigenstates. When the resonant coupling of an optically active transition with light is larger than the losses determining its linewidth, it becomes possible to spectroscopically resolve the resonant splitting due to the interaction. The system is then said to be in the strong light-matter coupling regime. Contrary to the weak coupling case, here the interaction between light and matter cannot be described in terms of emission and absorption of photons; it is instead necessary to consider the dressed light-matter excitations of the coupled system. Finally if the coupling becomes even larger, comparable with the bare frequencies of the excitations, we enter a third regime, called ultrastrong coupling. Such a non-perturbative regime was achieved for the first time in 2009 by my collaborators and I using intersubband polaritons [2], and has since been studied both theoretically and experimentally in a variety of different systems [3-6]. My group is at the forefront of the exploration of this fascinating regime in which, as light and matter lose their individuality and fuse in a single truly quantum object, a very rich phenomenology emerges [7-12].
[1] R. H. Dicke, Phys. Rev. 93, 99 (1954)
[2] A. Anappara et al., Phys. Rev. B 79, 201303(R) (2009)
[3] G. Scalari et al., Science 335, 1323 (2012)
[4] T. Schwartz et al., Phys. Rev. Lett. 106, 196405 (2011)
[5] T. Niemczyk et al., Nat. Phys. 6, 772 (2010)
[6] M. Goryachev et al., Phys. Rev. Applied 2, 054002 (2014)
[7] S. De Liberato, C. Ciuti and I. Carusotto, Phys. Rev. Lett. 98, 103602 (2007)
[8] S. De Liberato, Phys. Rev. Lett. 112, 016401 (2014)
[9] J. A. Cwik, P. Kirton, S. De Liberato, and J. Keeling, Phys. Rev. A 93, 033840 (2016)
[10] E. Cortese, P. Lagoudakis, and S. De Liberato, Phys. Rev. Lett. 119, 43604 (2017)
[11] L. Garziano, A. Ridolfo, S. De Liberato, and S. Savasta, ACS Photonics 4, 2345 (2017)
[12] S. De Liberato, Nature Communications 8, 1465 (2017)
Mid-Infrared Nanophotonics with Phonon Polaritons
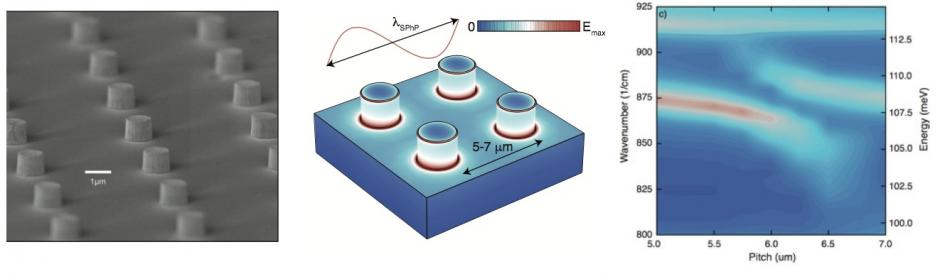
Left: SEM image of a SiC surface patterned by cylindrical phonon-polariton resonators. Center: COMSOL simulation of the resonator, showing the electric field intensity of the localised mode. Right: experimental reflectance map, highlighting the strong coupling (anticrossing) between the almost dispersionless localised phonon polaritons and the dispersive substrate surface modes as a function of the pillar distance. Images from Ref. [4].
Optical phonons at the surface of a nanostructured polar crystals can hybridize with light, creating mixed excitations called localized phonon polaritons. Those interface-bound excitations are in many regards mid-infrared analogous of localized plasmons supported by metallic resonators, but they absent themselves from the Ohmic loss characteristic of plasmonic systems. Localized phonon polaritons are developing into an innovative platform for mid-infrared quantum polaritonics. This is due to their extremely small mode volumes, long lifetimes, and large nonlinearities, as well as the relative facility to fabricate nanoresonators with features at the 100nm scale.
My group is leading the research in this innovative technological platform. We developed both analytical [1] and numerical [2] approaches to study linear properties of localised phonon-polariton resonators. We have also formulated a general nonlinear theory apt to describe polariton-polariton scattering that has for the moment been successfully applied to second and third order processes [3,4]. We also experimentally observed strong coupling between localised modes in the resonator array and propagative ones bound to the sample surface [5].
[1] C. R. Gubbin, S. A. Maier, and S. De Liberato, PRB 94, 205301 (2016)
[2] C. R. Gubbin, S. A. Maier, and S. De Liberato, PRB 95, 035313 (2017)
[3] C. R. Gubbin and S. De Liberato, ACS Photonics 4, 1381 (2017)
[4] C. R. Gubbin and S. De Liberato, ACS Photonics 5, 284 (2017)
[5] C. Gubbin, F. Martini, A. Politi, S. A. Maier, and S. De Liberato, PRL 116, 246402 (2016)
